AGI won't use computations
when patterns are enough ... like in brains
In a brain: “2+2=4” is a pattern to match, not a computation
“2+2=4” is an obvious example of pattern matching, rather than computation. Or is it? Isn’t everything computation? Or is everything combinations of patterns in a brain, but not necessarily the simplistic patterns some expect.
To get past the current limitations in AI, the next step towards Artificial General Intelligence (AGI) could emulate human brains. Patom theory shows the way forward with automatic pattern matching, rather than computation, to speed us towards AGI.
Today’s story comes from feedback (Quora reference here) on a Patom theory (PT) white paper I wrote. That post’s author claims pattern matching is wrong because the brain needs “logical reasoning and mental computation to … ensure accurate results.”
This newsletter argues that a brain operates without computation, as long as pattern matching is set up in the ‘right way’ like a brain with full automation and appropriate connections (links) between regions (pattern-storage).
Enabling AGI progress should start with a brain hypothesis
Before Patom theory, brain science operated without a clear scientific hypothesis on how a brain works. Note: saying that a brain is a computer isn’t a useful hypothesis since it isn’t specific enough. How would you falsify it?
Science progresses as hypotheses are defined and validated by testing. The parallels from astronomy come to mind, where the heliocentric model of the solar system eventually proved to be more effective than the geocentric one as confirmed by improved measurements and prediction capability.
What is AGI?
A machine qualifies as AGI if it’s capabilities are at the human-level on a broad range of tasks. For example, a machine that can safely drive a car, order products and services for you, and talk to you like a person, would be AGI.
We aren’t close to a machine that does that. No LLMs can drive cars, and driverless cars don’t generate text sequences. Neither are yet at human-level capability in their own domain. Therefore, we are not close to AGI.
What if simple patterns could be combined to identify complex patterns without loss, wouldn’t AGI follow? A ‘complex pattern’ could be how to answer a question based on an ongoing conversation - conversational AI. If each step can be done quickly and independently to the rest of the system, it can scale quickly.
Large Language Models (LLMs), by contrast, needs the entire system to operate correctly as a unit. That’s a tightly-coupled solution (a word needs the entire LLM to be resolved against new input) due to its machine learning (ML) roots.
Natural Language Understanding (NLU) is the best demonstration of the potential of Patom theory in AGI because manipulating meaning has complexity and scale. NLU is hard, some even said it is an NP-hard problem! That’s why it is an ongoing goal in the world of startups and IT giants despite a variety of expensive, unsuccessful approaches in its past.
What is computation? How do brains work?
In our quest to enable AGI, the debate over computation is critical.
What is computation? Digital computers are general-purpose machines that were designed around the technologies of the last century. There are problems with their design when it comes to replicating biological systems. That’s my excuse for the lack of progress in driverless cars and for human language systems not being at human level).
The relevant differences between brains and computers are that a computer:
lacks full automation like a brain: that is what programmers are for!
relies on instructions built into their design, and
uses memory inefficiently. A computer’s memory uses encoding and duplication; while Patom theory centralizes patterns. PT is so different that it could even eliminate the need for search engines!
A better approach for biological systems is one in which there is little or no need for a programmer, centralization of memory, and massively improved error correction in real-world applications (think much, much better Siri/Alexa/…).
Patom theory is an improvement over computational systems. It integrates patterns into a brain’s function. Pattern-matching more easily resolves errors than processing because matching valid templates against a noisy input can be powerful.
PT evolved from the question: “What if all a brain region does is store patterns and match them again?” Such a system could automate brain function, but it isn’t computation in a way like a digital computer, partly because memory isn’t arbitrary but complying with the laws of semantics.
What if all a brain region does is store unique patterns and match them again? Wouldn’t that automate brain function?
Patom theory claims patterns are behind all our brain’s capabilities and therefore, if correct, are central to AGI development. At their core, pattern-atoms (Patoms) enable the human-like capabilities we observe from language to complex motion control.
This is a breakthrough when compared to the computational model because it solves or explains previously unsolvable problems like parsing for Natural Language Processing (NLP).
Experts claim that brains compute. Do they?
We know how to process numbers on a digital computer. We encode numbers into a type, such as integer or real, and then pass the values into appropriate registers before executing an instruction and storing the result somewhere. Computers can perform instructions like addition, square root and cosine, depending on their design.
Brains differ from computers in many ways: their inputs and storage mechanisms for example.
To explain brains, the computing analogy has been used by well-known cognitive scientists like Steven Pinker and Gary Marcus. Is the brain the organ of computation? How would a brain process numbers similarly to the digital computer? I don’t know, but let’s see what has been proposed.
Steven Pinker: the brain is the organ of computation
Pinker wrote in So how does the Mind Work: “mental life consists of information processing or computation.”
Pinker qualifies his claim: “‘Computation’ in this context does not refer to what a commercially available digital computer does… a computational system is one in which knowledge and goals are represented as patterns in bits of matter (‘representations’).”
Gary Marcus: “Face It, Your Brain Is a Computer”
Marcus points out in his article: “Science has a poor track record when it comes to comparing our brains to the technology of the day.” He cites “hydraulic pumps”, “steam engines” and “holographic storage”. He leaves one out because it would undermine his article: “computers!” Haha, computers are the technology of the day!
Even if the Pinker and Marcus model is correct, how could we use it?
Computer memory versus brain memory
Digital computers were designed by people for general purposes (such as ballistics and accounting). It was decided to use encoded data to represent things in an agreed binary form. Even today, storage management ensures the correct interpretation of encoded data efficiently for things like integers, real numbers and strings.
This approach enables computer software to perform well at tasks from spreadsheets, to word processors, to the internet. In practice, data is allocated even in more complex ways by defining a class of data and what comprises it, such as a name (string) with its birthday (datetime).
This fundamental design of the digital computer results in the duplication of data, split from the processing Arithmetic-Logic Unit (ALU).
Think of it: data can be stored on disk, copied to a memory location for an update, then moved via a cache to a register to execute an instruction. Each representation is a copy of the original because data can be stored in any memory location due to its encoding. And your personal details may be stored in databases on the Internet, and on a mainframe computers by your suppliers, and on your mobile phone and PC and tablet. When you move house, many of those will be incorrect for a time.
Notice that such data is disconnected from the rest of the system. Pattern data in contrast is interconnected and fixed in the network.
This duplication and copying of information is efficient for traditional systems, but not normally so for biological ones. In contrast, our brains service information for only one person and appear to use a superior approach to avoid duplication, search and corruption.
The alternative memory model - hierarchical, bidirectional patterns
Do brains bring data to an area to execute instructions over it like a computer? No.
In Patom theory, brains evolved to (a) recognize patterns in senses and to (b) move muscles. Earlier brains from evolution are remarkably similar in many features with human brains and likely share common functions. Things like languages, mathematics, and labels like personally identifiable information came much later for humans.
A brain only needs pattern-matching for sensory experience and motion control, in theory, without a reason to send around encoded information. You can read the introduction to the PT memory model here which details the kinds of patterns that can be stored (the sets and lists representation).
By storing patterns in a fixed location, where they are first matched, we can access that pattern forever. That’s the definition of a pattern-atom. If we receive the same pattern, it is matched. Its subsequent signal, when matched, effectively represents the pattern downstream in the hierarchy via the bidirectional (reverse) link.
The Patom storage method enables far more information to be stored concisely than the computer’s version. Using a Patom label coud access all other associations (i.e. related knowledge). The cost of a single, atomic identifier is very low with this method and flexible as the hierarchy enables broad pattern selection (e.g. visual, auditory and so on).
If brains store and match patterns where they are found, there is no need to send around an encoded representation! Instead, a ‘match’ signals to a higher level - recognizing what is known against what is experienced at the lower level. e.g. ‘cat’ is a symbol made of ‘c’, ‘a’ and ‘t’ symbols. Brains interact with symbols in levels.
Evidence from brain damage supports the idea that brains store patterns in regions and build on them hierarchically. Such pattern atoms can be built out over time, effectively learning new distinctions while keeping the rest unchanged.
Here’s an example of the pattern flexibility needed. One day we may know that Brad Pitt is married to Jennifer Aniston, and the next we may know that he isn’t, even though he was. This context tracking seems subtle due to the changes in time (temporal dimension), but such models of context are necessary in the real world. In the brain, deleting data isn’t an option like in a computer database because human knowledge is far less lossy. Bidirectional access means efficient recognition of lossy input as it is easier to recognize a part of a known pattern.
Patterns are better than computation. While computers need to encode, copy typed data and execute instructions in programs, brains (patterns) are more versatile.
What is Patom theory?
Patom theory describes a way for brains to evolve to human level, such as for languages.
Introductory Examples
1. Brains can throw a ball
Consider the complexity of throwing a ball, an example of a robotic skill of the future and a fundamental capability of human brains.
What does a brain do to throw a ball (transcript - recorded in 1999)? We can consider throwing a ball as a complex pattern of muscle contractions and relaxations, with input from balance sensors from our inner ears and other proprioception. PT models the management of such motion as a sequence of patterns in the brain.
This differs from the computational explanation that the brain “plans the sequence of muscle contractions needed”. We learn to throw with improved accuracy by doing it, seeing the results and feeling our motion from the set of muscles activated in sequence. Storing and updating patterns and selecting the right ones again is PTs explanation for improved ball throwing.
2. The brain can see hidden triangles
In Kanizsa's triangle, there seems to be 2 triangles on top of 3 solid black circles. How can the brain recognize those elements when they are not physically there?
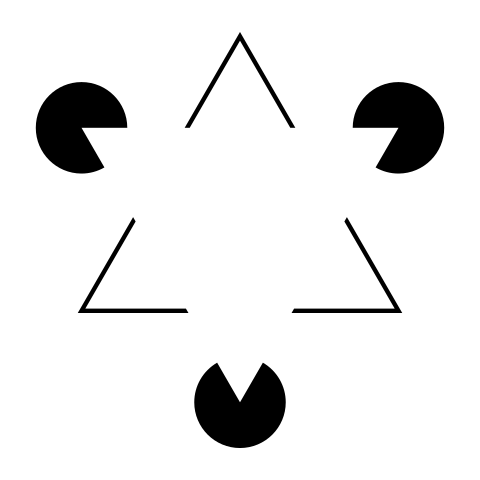
This example from the 1950s shows that our visual perception readily allows us to see shapes that are not ‘in the image.’ If we assume that the brain learns these shapes (triangles and circles) and their appearance in different situations, the recognition of the shapes follows from the matching of the triangles and circles in their understood situations (the triangle on top is blocking vision of the one underneath, and also the three circles).
A processing approach requires the system to ‘figure out’ that there are triangle shapes, somehow. How would that work? A pattern-matching exercise in the visual sense is trivial by just matching a set of templates.
This contrasts with a processing model where some program needs to address the recognition. How many programs are needed for rectangles, squares, stars and so on? How would that program be written? How would a brain learn it? The world of driverless cars awaits those human-level recognition skills!
Components of Patom theory
Patom theory aligns with brain evolution. Control of motion for survival, based on sensory feedback in an aware animal, starts it off.
To do that, all a brain needs is the ability to store, match and use hierarchical bidirectional linkset patterns. A linkset is a pattern made from a set of things, a sequence of things, or combinations of both.
As the patterns are linked, the elements are atomic because only a single version of any pattern is allowed in the brain. A second example would match the first stored one, not create a duplicate. Therefore there is no need for search, since each unit is a unique pattern. As more patterns become associated, higher patterns in the hierarchy become more complex because they are the increasing sum of multi-sensory patterns.
Pointing at some place in the network identifies the pattern atom (patom) that applies. In your brain’s visual memory could be the images of, say, your mother. All her visual patterns are associated together. Pointing back to this patom is a multisensory patom that holds the associations to the other sensory patterns (such as touch, olfaction, sound) for her. Much simpler animals to humans have had this capability to recognize multi-sensory aspects of objects for hundreds of millions of years. This approach allows a very concise representation of things, in which a single node in the network represents everything to do with it.
Evidence: how we teach children
As a brain-based approach, the methods we use to teach children should be something to emulate. It should also pose questions to answer: what does each step do for a child’s brain to learn?

The diagram above shows parallels between addition and language. Notice that a child’s brain learns the symbols in a predictable order.
The layers above show:
Input here is visual, as it is a written form. Vision must recognize written symbols that are learned by experience.
The symbols are combined into ‘words’, sequences that are subsequently learned through experience and then matched when found.
The ‘words’, not just their individual symbols, also connect to its meaning(s). These ‘words’ can be complex such as “4.242 x e^12” and “abso-bloody-lutely”. Meaning is a representation that is described by semanticists and includes relations like ‘kind of’, ‘part of’, and ‘restricted to’ that are in a network built by experience.
The meaning and words now can be combined with phrases made of them. Titles can be limited to words only (The Wizard of Oz), words and meaning, and meaning components only. Phrases allow generalization such as the syntax in mathematics or language, where many matching patterns are allowed.
Lastly, context provides specific cases where those patterns are recorded. “1+2=1” is valid syntax for addition, but the context is not valid, usually. (Imagine a course where synergy is defined as 1+1=3! Context is powerful)
Science of signs (semiotics)
The science of signs, known as semiotics (refer to the C.S.Peirce version) shows its influence in the above examples.
The concept to reinforce is this: the semiotics model starts with a sign (the letter, word or number above) that connects to its meaning that represents some real-world object. In language a sign can be some word, while its meaning is shown as a definition.
For this reason human beings learn the symbols/signs first (letters, other characters and numbers), which can then have meaning added. The symbols can be extended to more complex symbols as well, with new meaning (e.g. letter sequences to form words).
Our brains are learning to recognize in that order. This model forms a hierarchy as one thing (words) is built on top of others (characters).
In the examples that follow, notice how the resolution to symbols is made, but also consider how error correction is resolved. It is often easier to resolve an error by finding a higher-level match than to work out the lower-level one. Can you understand what the word ‘hte’ is in the phrase ‘hte cat’? Some would call this using context to resolve ambiguity.
Using Patoms in Examples:
Let’s look at two human-level examples of pattern-matching
Example 1: 2+2=4
In English, two plus two equals four. We can use a language pattern as well as a mathematical one! In English, “what is two plus two?” unambiguously asks for the sum. Children learn to add basic numbers in a sequence starting with counting. 1,2,3,4,5,6… This teaches the sequence pattern and identifies the relationship of the meanings of each numeral. Then they learn addition, then add subtraction and so on. The simplest patterns could be memorized or utilize a simple pattern (5+4 = 11111 + 1111 = 111111111 = 9 x 1s = 9). This example introduces pattern storage, matching and use.
Example 2: 223+68=?
For larger numbers, the syntax remains the same (number,’+’,number,’=’,number). Recognition of the numbers themselves is more complex with commas, periods and even exponents possible. The ‘process’ to add multi-digit numbers together is still just a sequence of pattern steps. As Patoms can be sets and sequences, larger numbers remain consistent with the pattern-matching theory.

Example 3: “The man Beth saw saw the car John saw”
The patterns we saw for addition can be summarised as (a) convert the symbol(s) to their meaning, then (b) seek a pattern(s) that performs the steps to get a result (c) apply the pattern(s) and (d) repeat until no more patterns are matched.
Here we see an English sentence that embeds other sentences. This level of complexity is typical of human language, in which the internal phrases should be resolved before the rest of the sentence (they are constituents). The full sentence means ‘the man saw the car’. There is more context available, of course. Which car? The one that John saw. Which man? The one Beth saw.
The longer given sentences are, the more accurately the information tends to be conveyed.

The Pat Inc. semantics engine resolves the example by recognizing the internal phrases first and then the full sentence. This approach will retain some ambiguity that is best resolved with the full context, as people’s brains do.
Language is exquisitely precise as in this example to pack information into phrases.
So what? Not just theory, PT works!
In 2017, a Patom-based system performed with a perfect score for Facebook conversational tasks (a deep learning benchmark). Its pragmatics engine has successfully answered complex questions, such as the embedded sentence examples above, using only meaning representations. That technology promises to become the basis of lossless knowledge repositories in the future, removing individual languages as an impediment to communications. In short, it works in theory and in practice!
Conclusion
A scientific theory allows for validation and continuous improvements over time. Patom theory as described above was created as a pattern-matching system because it is effective at answering a number of otherwise unsolved questions. It has also proven to be effective at solving problems in NLU and conversational AI to earn world’s first status at working with meaning in context using the new, automated approach.
By using a theory such as Patom theory to explain human brain function, AGI development, whose function requires improved biological capabilities, could accelerate past current limitations. Then AGI will usher in those applications we are all waiting for like driverless cars and machines that we can talk and write to using the last interface we’ll ever need - human language.



