How '2+2=4' works for better AGI

Explaining pattern-based arithmetic in detail

1. Pattern matching: way better than computation

I’ve been working on the technique to parse from text to meaning to knowledge for many years incorporating the science of semiotics (signs). One of the goals of these substack newsletters is to help others to understand the approach. About the last article, a wise x.com user told me:

“Read all that, but... seems like basic logic is still used (add, compare, etc).” (thanks to sd_marlow!)

OK. I thought I explained why computation is not needed in brains, but I left some steps out. Hey, I knew what I meant! Here is an improved explanation, with diagrams.

How Matching Works After Learning

Diagram 1: Adding knowledge once the system has learned how to do addition. Moving from (I to V) uses stored patterns. Future AGI systems can focus on knowledge, trusting the provision of it.

In Diagram 1, our brain recognizes input (I) as signs. The match (II) is connected to more extensive patterns that include the meaning of the sign. The meaning connects to emergent sequential patterns (III) that, in turn, resolve the meaning (IV). This meaning is stored as knowledge (V) with the current context.

AGI needs a model

Language and brains seem hard, but most things do — until we understand them.

Artificial General Intelligence (AGI) doesn’t seem to be progressing. Is it the fundamental approach that is holding it back? Can’t we just find a better algorithm or improved mathematical model? Where would that start?

We can improve the path to AGI by changing focus from the computational paradigm. Given what we know about the human brain’s function, computation doesn’t fit in.

We see that human brains evolved from earlier ones demonstrating the key to AGI: sensory recognition and motor control. How much easier would driverless car design be with vision and motor control of a leopard? In addition, human brains learn language and mathematics. Is language and math a human-only skill, or it is just an incremental improvement?

We should focus on the symbolic solutions that Patom theory (PT) demonstrates, based on Role and Reference Grammar’s (RRG) linguistic model.

Language and math can be complex. RRG linguistics taught me the building blocks of languages: referents (things in the world) and predicates (relations between things). Amazingly, the RRG linking algorithm allows the nucleus of the sentence to be either. Languages support the precision and flexibility needed for language learning. Note: today’s examples exploit some RRG explanations that are otherwise hard to discover.

2. Diagram with Learning for Discussion

Diagram 2: Patom model showing how arithmetic can be performed without any computation. The linked set and/or sequence patterns are stored, matched and used.

In Diagram 2 the kinds of patterns needed to learn and use addition are shown. There is no computation needed.

I. Vision. Input is received in the visual sense. Note that there are commonly multiple signs that communicate the same thing, as shown (e.g. 2=ii).

II. Recognize Sign. Stored patterns, the signs in a semiotics model, match the input.

III. Link Meaning. To learn the symbols, a meaning atom is created (or found) and then linked to the sign.

IV. Link Category. Our brain through communication such as language receives: “that’s the number 2”. This meaning adds a hypernym relationship (i.e. two is a kind of number).

V. Recognize Emergent Syntactic Pattern. Once our brain has the hypernym association to number, repetition of patterns consolidates sequence: ‘number + number’. Patterns cannot be repeated (they are atomic in the sense they are irreducible and can’t be duplicated. A link allows its use as building blocks for other patterns).

VI. Use Linking Algorithm. The Role and Reference Grammar (RRG) linguistics uses a syntax to semantics algorithm (and back) that we adopt here. The syntax in language differs from the mathematical syntax, but their meaning is the same as shown for ‘equal’ and ‘plus’. A semantic representation, determined by the predicate, starts from the syntax.

VII. Store Context/Knowledge. The recognition of combinations of predicates like ‘+’ and ‘=’ result in the embedded representations shown. Context, or knowledge, is the consistent environment that includes the semantic representations. An adult’s memory would include a number of related examples (e.g. childhood rote teaching).

No computations needed

In Diagram 2, there are no computations: there is no need for something like it to get the job done because patterns are sufficient.

Note that Patom theory explains what a brain does, not how it does it. At a high level, a brain matches patterns that represent objects in the world, often using the mature science of signs.

3. What is learned?

Let’s look at the steps in Diagram 2 to see what makes it work. There are two parts to the operation: (a) learning and (b) operating at each level. Matching patterns is a given: the theory of brain regions storing sets and sequences of patterns.

Vision

Sensory apparatus, like vision in animals, has evolved into very efficient machines over tens or hundreds of millions of years. They provide a well-tested input to the brain. Like muscles that contract with appropriate sequences, this isn’t computation in the sense of a digital computer.

The brain’s great ability is to take disparate kinds of sensor input and motor output and control it with the same kind of brain materials — the pattern-store within a brain region. This capability signals the ‘G’ in AGI if we can emulate it.

Sign Recognition: link to Meaning (Interpretants)

Stored patterns compare the input received. If a match is made, they signal. By themselves, they do nothing. They are probably ambiguous at this level.

The match of a sign signals with its links. (Phrase pattern emergence comes from generalized meaning from these links). Learning involves linking the sign with meanings. There can be many signs that activate a meaning (e.g. ‘2’ and ‘ii’ activate the meaning ‘r:two’).

As children, learning numbers involves recognizing the numerals first. Follow me: 0,1,2,3,4,5,6,7,8,9! Although there is value in recognizing the numerals and their order, without meaning and further associations, sign-only capabilities are limited.

Our brain associates ‘2’, the sign without meaning, with meaning by linking it to an interpretant ‘r:2’.

I use a convention for elements in the meaning layer. The ‘r’ in the label shows that we are adding the element as a referent (a thing) rather than a predicate (a relation of things, ‘p’). In semantics, a ‘kind of’ relationship or hypernym is a more general meaning of the interpretant, so ‘r:2’ is given a hypernym of ‘r:number’ (i.e. 2 has the hypernym ‘number’).

So when we recognize a ‘2’ in Patom theory, its match uses the links ‘r:2’ and its hypernym ‘r:number’. Many more associations will be established over time (‘2’ is a digit, a number and a numeral!).

Syntax to Semantics Linking

The meaning layer enables the combinatorial increase in variation of word form sequences. It allows multiple words to be substituted in sentence sequences. Sensory experience activates the meaning element the same way that its sign does in auditory (speech) or visual (reading) senses.

Emergence of phrases

The creation of syntax is still required. The meaning layer in this example can be exploited. A hypernym (kind of) relationship to ‘r:2’ is ‘r:number’. So what?

The emergence of syntax comes from the model shown. By storing meaning details, a range of possible phrases emerge from re-use. We all recognize that the phrase:

{ number plus number }

comes from samples like 1+2 and 10+98. Patom theory makes this emergent by limiting the number of phrase patterns to 1 per brain (for many reasons).

For: 1+1 you can imagine seeing a number of examples: 1+1, 1+2, 1+3, … 3+1, 3+2, … Each time we get one of those patterns, their hypernyms are being activated. So 1+1 is also {number + number}, and 1+2 is {number + number}, and 3+2 is {number + number}. The phrase pattern, {number + number} emerges.

How does a brain get the next step: its semantic representation?

Linking to meaning

The RRG linking algorithm sets the structure of a semantic representation based on its predicate class. Depending on the syntax received, arguments are assigned positions. The principle works the same way with mathematics as with human language.

‘+’ means plus which would be written in semantics as: plus'(1,1).

‘=’ means equals which would be written in semantics as: equal'(x,y).

When we combine these together with 1+1=2, we get: equal'(plus'(1,1),2))

Let’s run through a full example.

Now when we see 4+5=9, the meaning of ‘4’, ‘5’ and ‘9’ each link to ‘r:number’. As a result, the {number + number} pattern is matched creating: plus'(4,5) and then number = number matches equal'(x,9) provided plus'(4,5) is also a number.

This input therefore activates equal'(plus'(4,5),9).

Innate meaning

RRG models all human languages: semantics comes from syntax within discourse pragmatics and back again.

There are wild variations across languages for what that looks like - different words, phones (sounds), phrase orders and so on, but our brains are capable of learning any language because they can recognize the universals like the layered clause and reference phrase.

The RRG analysis of “2 is a number” is a classificational sentence, meaning ‘2’ is being classified as a kind of number.

The semantic representation is be’(2, [number’]) — i.e. 2 has the attribute, number.

To get from word order (syntax) to a semantic representation (meaning), RRG uses universal phrase templates that constrain language-specific templates.

Why do these templates exist? That’s a job for the future from semanticists who will also research brain regions, but a key element must be how a human brain’s anatomy is setup that allows these languages to be understood. It’s the gift of helpful anatomy to a pattern-matching system.

4. Discussion

Adding Bigger numbers together

The syntax to match larger numbers is unchanged, as ‘1’ and ‘143’ are both numbers in the meaning layer and match the specified phrase pattern. Diagram 3 shows a simple implementation to add larger numbers together, which could apply to any number of arbitrary length.

The use of the semiotics types of signs (icon, index and symbol) enables brain flexibility for tasks. Addition of large numbers, using semiotics’ icon signs, is shown combining ‘rote knowledge’ to work out more complex results.

The boxes below hold single digits 0-9, with the icon (the diagram that aligns the numerals from input numbers). The knowledge of addition (0..9 + 0..9) directs the ‘addition’ pattern. Again, patterns can be either sets or sequences.

Diagram 3: Another kind of sign is an icon. Here, the diagram (an icon) on the left works with a common pattern to perform addition. Each step can rely on simple addition to update the diagram including a ‘carry’

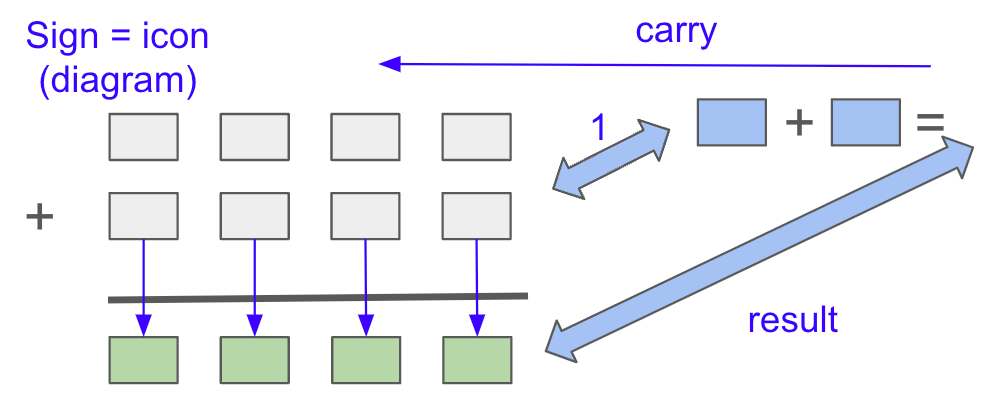
Note that the manipulation of the symbols relates to the meaning layer, not the sign layer. The ability to add ‘ii’ ‘+’ ‘ii’ relies on the meaningful element labeled r:2 above, not the sign ‘ii’. Using signs limits generalization excessively in combinatorial systems like human language and mathematics.

Error correction

Brains integrate error correction in operation. How does that work?

In linguistics, a principle is that predicates determine their arguments. You can see it in the addition example. This does NOT make sense:

‘123+cat=’

because the phrase pattern we are experienced with, ‘number + number’, is not matched (‘cat’ doesn’t have a hypernym of ‘r:number’).

This is the concept of “selectional restriction” in which each argument of ‘+’ must be a number. Similarly, the arguments of ‘=’ are also numbers.

If the sequential pattern isn’t matched, there is no creation of a semantic representation. It’s like not knowing a language. If you can’t recognize the words or phrases, your brain can’t understand the language.

Knowledge

The diagrams shows how a brain could do arithmetic with only pattern-matching. The actual addition can take place from the knowledge repository (memorised) or by adding up by counting (2 + 2 = 1+1+1+1=4).

From what we saw, 2+2=4 starts with the recognition of the numbers. Next a pattern matches the syntax for 2+2. Then a pattern matches the syntax for number = 4.

The semantic representation is therefore equal'(plus'(2,2),4). But is it true?

To add knowledge, a brain expects a source (context!) to deal with alternative possibilities. “Where did this claim come from?” checks context.

• John said, “2+2=4”. Or

• For a team’s synergy, the teacher says that “1+1=3”.

Knowledge is how a brain stores with consistency from experience—with its meaning, not its signs.

Our brain is constantly learning, unlike today’s LLMs. If we don’t have particular knowledge, we can use patterns to follow a path to the right results.

5. Conclusion: Brains don’t need computation

Brains don’t compute: matching patterns is enough. That’s Patom theory - a model that explains what a brain does, rather than how it does it.

If addition doesn’t need computation, and human language doesn’t, we can focus on the patom approach to progress towards AGI (human-level capabilities on machines)!

My company, Pat Inc., has demonstrated the capability to parse language in real-time using a sequence quite similar to today’s example. Using this new approach, there is an opportunity to improve the interactions between humans and machines in real-time to help usher in AGI.